Hace un par de días les mencionaba la forma de obtener la Ley de Cosenos a partir del producto Punto, esta ves veremos la Ley de Cosenos a partir del producto Cruz.
Es conveniente saber que el producto cruz es algo muy distinto al producto punto o a una multiplicacion cualquiera, pues es una operación entre vectores donde se obtienen vectores, donde el producto es un tercer vector perpendicular a los dos vectores de origen. Por el momento, la forma vectorial del producto cruz no nos importa, nos centraremos en la forma vectorial que esta dada por el producto de las magnitudes de ambos vectores por el seno del angulo entre ellos por un vector. En lenguaje humano, esto es:
Ahora entremos 100% en materia de ley de senos. Usando una combinación lineal, obtenemos que
Ahora, como sabemos que debemos tener un mecanismo que nos permita relacionar la magnitud de cada lado con su respectivo angulo y que este sea igual a la mima relación entre los demás lados y sus ángulos, comenzamos multiplicando en cruz a ambos lados de la igualdad.
Gracias a que el producto cruz tiene propiedades distributivas, obtenemos:
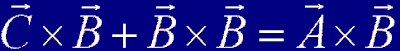
Cabe aclarar que al multiplicar un vector en cruz por el mismo vector, obtenemos cero. Esto es una consecuencia del producto cruz en su forma vectorial (que abordaremos en otro momento). En un intento de máxima flojera que espero entienda usted, querido lector, he desarrollado la forma geométrica del producto cruz al mismo tiempo que he tachado a ambos vectores resultantes y a la magnitud del vector B, mejor conocida como el lado B, pues si los despejamos estos se eliminan
Luego de haber eliminado
[aplausos]Espero que les sirva de ayuda esta demostración y que, a los lectores mas habituales de este blog, no se molesten por tener que soportar estas cosas mas frikis. Un saludo a todo mundo!!!
No hay comentarios:
Publicar un comentario